1. 알고리즘의 정의
= 문제를 해결할 수 있는 잘 정의된(well defined) 유한(finite)시간 내에 종료되는 계산적인(computational) 절차(procedure)
- 입력을 받아서 출력으로 전환시켜주는 일련의 계산절차
- 알고리즘은 프로그램의 엔진에 해당하는 중요한 절차이다

2. Algorithm vs Method
Algorithm: 유한 시간 내에 종료됨
ex) 순차 검색, 이분 검색
Method: 유한 시간 내에 종료되는지 모름
3. 문제의 표기 방법
문제
: 답을 찾고자 던지는 질문
파라미터 (parameter, 매개변수)
: 문제에서 특정값이 주어지지 않은 변수
문제의 사례 (instance) (입력)
: 파라미터에 특정 값을 지정한 것
사례에 대한 해답 (solution) (출력)
: 주어진 사례에 관한 질문에 대한 답


4. 알고리즘의 표기 방법
1) 자연어
: 한글 또는 영어
– 문제를 정확하게 기술하는데 어려움 있음.
- 상대적으로 긴 문장이 필요. 해석하는 사람에 따라 다르게 해석할 가능성 존재
2) 프로그래밍언어
: C, C++, Java, ML 등
- 문제를 정확하게 기술할 수는 있음.
– 너무나 구체적인 기술을 해야 하므로, 알고리즘을 이해하는데 어렵고 복잡함
3) 의사코드(pseudo-code) => 우리는 이걸 많이 쓸 예정!
: 이 강의에서는 C++에 가까운 의사코드를 사용한다.
- 직접 실행할 수 있는 프로그래밍언어는 아니지만, 거의 실제 프로그램에 가깝게 계산과정을 표현할 수 있는 언어
(의사(疑似): 실제와 비슷한) ✓ 의미전달에 문제가 없을 경우에는 축약된 형태의 코드로 표시
- 간결하면서도 정확한 의미 표현 가능 알고리즘은 보통 의사코드로 표현한다.
4) 흐름도




5. 알고리즘의 정확도 분석
= 알고리즘이 의도한 대로 수행되는지를 증명하는 절차
정확한 알고리즘이란 모든 입력에 대해 유한시간 내에 정확한 답을 출력하는 알고리즘
(정확하지 않은 알고리즘이란 무한시간 or 정확하지 않은 답 출력)
6. 알고리즘의 종류 및 비교
1) 순차검색 알고리즘
2) 이분검색 알고리즘
: 크기가 n인 배열 S에 x가 있는가? [n, S[], x / location]
단위 연산: 배열의 아이템과 키 x와의 비교 연산 (S[location] != x)
최악의 경우: W(n) = n
= x가 배열의 마지막 아이템이거나, x가 배열에 없는 경우 단위 연산이 n번 수행된다.
평균의 경우 ( x가 S[] 내에 있는 경우): A(n) = n+1/2
평균의 경우 ( x가 S[] 내에 없는 경우): A(n) = n(1-p/2) + p/2
최선의 경우: B(n) = 1
: 크기가 n인 정렬된 배열 S에 x가 있는가? [n, S[], x / location]
최악의 경우: lg n + 1

3) 배열 덧셈
: n개의 수로 된 배열 S에 있는 모든 수를 더하라 [n, S[] / sum]
단위 연산: 덧셈 / 모든 경우: T(n)=n
단위연산: 지정문 / 모든 경우: T(n) = n+n+1
4) 교환정렬
: 비내림차순(nondecreasing order)으로 n개의 키를 정렬하라 [n, S[] / S[]]
단위연산: 조건문 (S[i]와 S[j] 비교) / 모든 경우: T(n)=(n-1)n/2
단위연산: 교환하는 연산 (exchange S[i]와 S[j]) / 최악의 경우 : W(n) = (n-1)n/2
= 조건문이 항상 참(true)이 되는 경우 ( = 입력 배열이 거꾸로 정렬되어 있는 경우 ex. 54321)
5) 행렬곱셈
: 두 개의 n x n 행렬의 곱을 구하라 [n, A[][], B[][] / C[][]]
단위연산: 가장 안쪽 for 루프에 있는 곱셈 (i, j, k)/ T(n) = nxnxn = n^3
6) 피보나찌 수열 구하기 (재귀법-피보나찌에서는 더 비효율적)
: n번째 피보나찌 수를 구하라 [n / fib(n-1)+fib(n-2)]
계산하는 항의 총 개수: T(n) > 2^(n/2)
*정리: 재귀적 알고리즘으로 구성한 재귀 트리의 마디의 수를 T(n) 이라고 하면, n >= 2인 모든 n에 대하여 T(n) > 2n/2 이다.
7) 피보나찌 수열 구하기 (반복법)
:n번째 피보나찌 수를 구하라 [n / fib(n-1)+fib(n-2)]
계산하는 항의 총 개수: T(n) = n + 1 [중복 계산이 없음]
*즉, f[0]부터 f[n]까지 한 번씩 만 계산

6. 알고리즘의 복잡도
= 알고리즘의 복잡도를 어떤 방식으로 표현할지에 대한 이야기
공간복잡도 분석 (space complexity)
= 입력 크기에 따라서 메모리가 얼마나 필요한 지 결정하는 절차
시간복잡도 (time complexity) [더 중요]
= 입력 크기에 따라서 단위연산이 몇 번 수행되는지 결정하는 절차
*입력 크기 = 배열의 크기, 리스트의 길이, 행렬에서 행과 열의 크기, 트리에서 마디와 이음선의 수
*단위 연산 = 비교문(T/F), 지정문(변수에 값을 할당) 등을 의미

7. 알고리즘 분석 방법의 종류
1) 모든 경우 분석 Every-case analysis
2) 최악의 경우 분석 Worst-case analysis O
3) 평균의 경우 분석 Average-case analysis Θ
4) 최선의 경우 분석 Best-case analysis Ω
*2(최악),4(최선)는 쉬움, 3(평균)은 어려움 ->가장 중요한 분석 방법은 2(최악)임
ex) 최선의 값을 0.1로 뒀음. 그런데 100번 중 99는 0.01초, 1번은 100초가 걸려서 평균이 0.1초가 나옴.
-> 평균(0.1초)가 뭐든 최악(100초)이 뭔지를 알아야 해결해서 피할 수 있음

8. 정확도 분석
= 알고리즘이 의도한 대로 수행되는지를 증명하는 절차
정확한 알고리즘이란?
✓ 어떠한 입력에 대해서도 답을 출력하면서 멈추는 알고리즘
9. 복잡도 함수
= 알고리즘의 복잡도를 나타내는 함수로, 음이 아닌 정수(input)가 주어지면 음이 아닌 실수(output)를 내어줌
(단위 연산 횟수나 수행 시간은 음이 아닐 수밖에 없음)
-> 복잡도 함수는 높은 차수항이 궁극적으로 지배함!!
o(최상한/small-O) O(상한) Θ(평균) Ω(하한) ω(최하한/small-Ω)
[오른쪽으로 갈수록 최선의 경우, 아래쪽에 있는 그래프가 cf(n)]
[왼쪽으로 갈수록 최악의 경우, 위쪽에 있는 그래프가 cf(n)]


대표적인 복잡도 함수
복잡도 함수 그래프에서 아래에 있는 함수(낮은 차수항)일 수록 빠르고 좋다


9-1. Big-O 표기법 -최악의 경우 (cf(n)이)
점근적 상한으로 표기
점근적 상한 = 주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ O(f(n))이면, n ≥ N인 모든 정수 n에 대해서 0 ≤ g(n) ≤ c×f(n)이 성립하는 양의 실수 c와 음이 아닌 정수 N이 존재한다.
* g(n) ∈ O(f(n)) 읽는 방법: g(n)은 f(n)의 Big-O
즉, N, c가 특정한 값일 때, g(n)은 c f(n)보다 궁극적으로 좋다(빠르다)고 할 수 있다

어떤 알고리즘의 시간복잡도가 O(g(n ))이라면
✓ 입력의 크기 n에 대해서 이 알고리즘의 수행시간은 아무리 늦어도 c f (n)은 된다. (cf (n)이 점근적상한이다.)
=> 이 알고리즘 g(n)의 수행시간은 cf (n)보다 절대로 더 느릴 수는 없다.
[예시]
1. 성립 O 2. 성립 X



9-2. Ω 표기법 - 최선의 경우 (cf(n)이)
(최악의 경우인 Big-O와 반대)
점근적 하한으로 표기
점근적 하한 = 주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ Ω(f(n))이면, n ≥ N인 모든 정수 n에 대해서 g(n) ≥ c×f(n) ≥ 0 이 성립하는 양의 실수 c와 음이 아닌 정수 N이 존재한다.
* g(n)은 f(n)의 오메가
즉, N, c가 특정한 값일 때, g(n)은 c f(n)보다 궁극적으로 나쁘다(느리다)고 할 수 있다
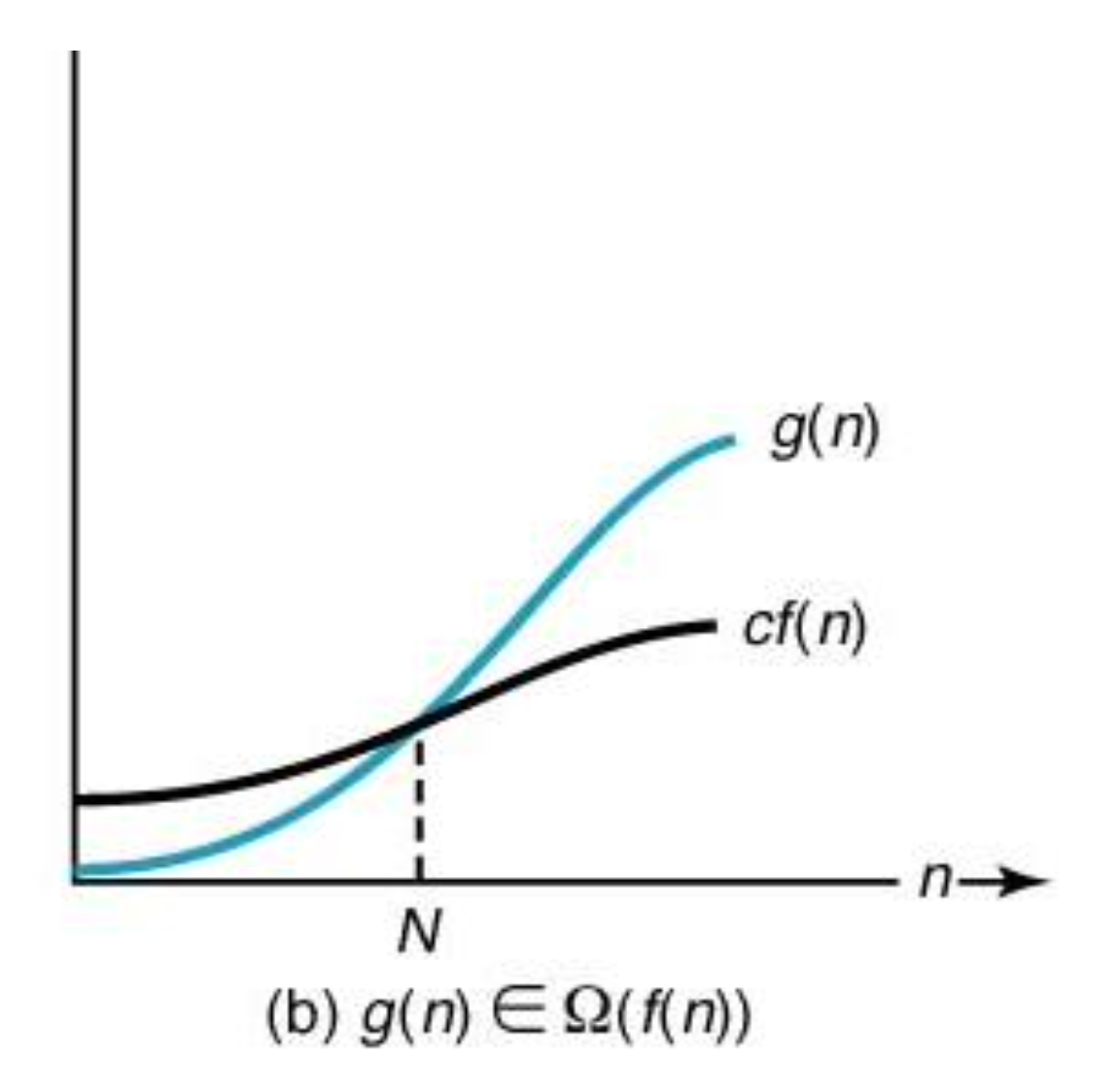
어떤 알고리즘의 시간복잡도가 O(g(n ))이라면
✓ 입력의 크기 n에 대해서 이 알고리즘의 수행시간은 아무리 빨라도 cf(n)이다. (cf (n)이 점근적 하한이다.)
=> 이 알고리즘 g(n)의 수행시간은 cf (n)보다 절대로 더 빠를 수 없다.
[예시]
1. 성립 O 2. 성립 X


9-3. Θ 표기법 - 평균의 경우(df(n)과 cf(n)의)
점근적 상한과 점근적 하한의 교집합으로 표기
주어진 복잡도 함수 f(n)에 대해서 Θ (n) ∈ O(f(n)) n Ω(f(n))이면, n ≥ N인 모든 정수 n에 대해서 c x f(n) ≤ g(n) ≤ d×f(n) 이 성립하는 양의 실수 c와 d, 음이 아닌 정수 N이 존재한다.
*읽는 방법: g(n)은 f(n)의 차수
즉, g(n)은 궁극적으로(점근적으로) Big-O(상한)과 Ω(하한)의 사이에 있는 것을 의미함
= 쉽게 말하면 평균적인 복잡도의 느낌!

[예시]
1. 성립 O

9-4. small-O 표기법 -최최악의 경우 (cf(n))이)
(Big-O 보다 멀리있는 상한을 나타냄)
복잡도 함수끼리의 관계를 나타내기 위한 표기법
= 주어진 복잡도 함수 f(n)에 대해서 g(n) ∈ O(f(n))이면, 모든 양의 실수 c에 대해 n ≥ N인 모든 정수 n에 대해서 0 ≤ g(n) ≤ c×f(n)이 성립하는 음이 아닌 정수 N이 존재한다.
* g(n) ∈ O(f(n)) 읽는 방법: g(n)은 f(n)의 Small-O
즉, N이 특정한 값일 때, g(n)은 c f(n)보다 궁극적으로 훨씬 좋다(빠르다)고 할 수 있다

[Big-O와 Small-o의 차이점]
- Big-O : 실수 c > 0 중에서 하나만 성립하여도 됨
- Small-o : 모든 실수 c > 0에 대해서 성립하여야 함
9-4. ω 표기법 - 최최선의 경우 (cf(n))이)
(small-Ω =ω / Ω 보다 멀리있는 하한을 나타냄)
복잡도 함수끼리의 관계를 나타내기 위한 표기법
* g(n)은 f(n)의 small-오메가
즉, N, c가 특정한 값일 때, g(n)은 c f(n)보다 궁극적으로 훨씬 나쁘다(느리다)고 할 수 있다

응용 문제 풀이
전체적으로 성능은 cn > cn^2 > 2^n 순서대로 함수의 차항이 낮을수록 빠르고 좋다


1번 vs 2번
= 복잡도 cn와 cn^2 중에서는 cn이 더 빠르지만 cn^2을 처리하는 기계의 처리 속도도 2배에서 4배로 더 빨라졌으므로 결국 같은 크기인 2m개의 문제를 해결할 수 있는 것이다.
1번 vs 3번
= 복잡도 cn^2와 c2^n중에서는 cn^2이 더 빠르다. 만약 둘다 처리속도가 4배였어도, cn^2은 2m개, c2^n은 m+2개로 차이가 날 것이다.